Where are Coronal Loops Heated?
Where are Coronal Loops Heated?
Science Nugget: June 29, 2001
The Million-Dollar Question: Is the corona heated from the top or
bottom, or uniformly?
Answer: Previous results give a very mixed answer, but a
reconciliation may be in sight. Read on!
Coronal heating is one of the Big Questions of solar physics. Simply put,
this is because understanding how the energy gets transported to the upper
atmosphere and deposited there is crucial to figuring out such fundamental
things as how the solar wind is accelerated, and why coronal loops are
hot. The problem of heating coronal loops has been attacked innumerable
times since its discovery 60 years ago, and a handful of reasonable
mechanisms have been explained. These explanations are not without their
shortcomings, however, and one can safely say that we still don't now
precisely how all the pieces fit together. This week, we will examine in
detail one aspect of the mystery: Where are the coronal loops heated?
The argument here, which focuses primarily on the cooler loops in the
corona (i.e., less than about 3 million kelvins) is based on a paper just
submitted to Astrophysical
Journal by Markus Aschwanden; a preprint can be found here
(PostScript format).
History of Yohkoh Results
 For part of his Ph.D. thesis, Carl Foley analyzed a loop system observed
with
Yohkoh on 3-Oct-1992 (see figure at right) and found that the
filter-ratio temperature increases with altitude along the loop.
This result prompted a Letter in Nature by Priest et al.
(1998) that announced:
For part of his Ph.D. thesis, Carl Foley analyzed a loop system observed
with
Yohkoh on 3-Oct-1992 (see figure at right) and found that the
filter-ratio temperature increases with altitude along the loop.
This result prompted a Letter in Nature by Priest et al.
(1998) that announced:
"From a comparison of the observations and models
we conclude that uniform heating gives the best fit
to the loop temperature distribution, enabling us
to eliminate previously suggested mechanisms of
low-lying heating near the footpoints of a loop.
Our findings favour turbulent breaking and reconnection
of magnetic field lines as the heating mechanism of the
diffuse solar corona".
With that, the coronal heating problem seemed to be almost solved!
A major paper (Priest et al. 2000) followed with
elaboration on the temperature model fits. However, soon after, a critical
paper by Duncan MacKay et al. (2000) found some problems
with the previous analysis, mainly that the error bars of the filter ratio
temperatures seem to be underestimated, and also that the temperature
model used in the paper by Priest et al. had no transition region, so the
footpoints of the loops needed to be located some 100,000 km inside the
Sun to make a uniform heating model fit. Just trying to match the
footpoint positions to the limb, where they had been observed with Yohkoh,
made MacKay conclude that a footpoint heating model would be more
consistent with the data, although it did not provide a better fit. So,
the dilemma stayed in the air, that no model seemed to fit the
Yohkoh data.
Contradictory results from TRACE ?
An extensive analysis of some 40 TRACE loops, for which the temperature
and density were measured along their length, revealed that in order to
achieve a balance between heating (energy input), radiative loss (energy
output), and conductive loss (output), the heating must be concentrated at
the footpoints, with a scale height of only 10--20 megameters
(Aschwanden et al. 2000). This is exactly the
opposite of what was found from Yohkoh loops. Is there a
contradiction?
An Attempt at Reconciliation
In addition to placing the loop footpoints some 100 Mm inside the Sun, a
recent re-analysis of the 3-Oct-1992 loop system points out another
apparent problem with the uniform heating model. In order to satisfy a
commonly used scaling law (i.e., Rosner, Tucker, and Vaiana
1978) with uniform heating, and to simultaneously account for the
brightness of the 3-Oct-1992 loops in the Yohkoh images, the column
depth of emitting plasma needs to be something like 10^15.4 cm. This
corresponds to looking lengthwise along an arcade that is 36,000 solar
radii long!
However, if one applies the footpoint heating model, say with a heating
scale height of 15 Mm, one solves two problems at once:
- The temperature solution climbs very quickly from transition region to
coronal temperatures, so that the "submersed footpoint problem" of the
uniform heating model disappears.
- The base pressure bumps up by a factor of 685 according to the scaling
law of Serio et al. (1981). Since the emission of X-rays
is related to the square of the plasma density, the emission will be
increased by a factor of about 500,000. This means that the column depth
of plasma required to account for the observed brightness is less than one
solar radius, which is manageable for large loop arcades.
However, a single-fluxtube model with footpoint heating still does not
fit the data. We have to go one step further and include at least two
different temperature components in the model, say hot loops with an apex
temperature of 2.6 MK, embedded in a cool background corona of 1 MK, and
then we obtain a pleasing fit to the filter-ratio temperatures and fluxes
in both filters, with physically acceptable values for the loop densities
and column depths (see figure below), for a heating scale height of 13 +/-
1 Mm.
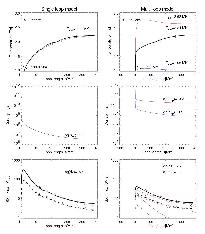
Moral of the Story
The Yohkoh and TRACE results can be reconciled if data analysis is
done with proper treatment and interpretation of the filter-ratio
temperatures. Even more important is to include the X-ray fluxes in the
analysis, because the emission measures provide important constraints on
the densities, column depths and radiative losses, information that cannot
be obtained from the filter-ratio temperatures alone. The filter-ratio
temperatures should be interpreted as "emission-measure weighted
temperatures", and therefore, they will always increase with height in
Yohkoh data, because of the hydrostatic weighting bias (pointed out
in a Letter by Aschwanden & Nitta, 2000).
As we stated above, the argument here is based on a paper just submitted
to
Astrophysical Journal
by Markus Aschwanden; a preprint can be found here, in
PostScript format.
June 29, 2001
M. Aschwanden
<aschwand@lmsal.com>;
edited for the web by
D. McKenzie
<mckenzie@isass1.solar.isas.ac.jp>.
 For part of his Ph.D. thesis, Carl Foley analyzed a loop system observed
with
Yohkoh on 3-Oct-1992 (see figure at right) and found that the
filter-ratio temperature increases with altitude along the loop.
This result prompted a Letter in Nature by Priest et al.
(1998) that announced:
For part of his Ph.D. thesis, Carl Foley analyzed a loop system observed
with
Yohkoh on 3-Oct-1992 (see figure at right) and found that the
filter-ratio temperature increases with altitude along the loop.
This result prompted a Letter in Nature by Priest et al.
(1998) that announced:
